An e-graph compactly represents many equivalent programs. Commonly used in Equality Saturation and modern theorem-provers.
It’s a data-structure that represents equivalence relations over terms.
It is made up of equivalence classes (or e-classes) which are sets of equivalence nodes (e-nodes). e-nodes are n-ary operators from whatever domain you are operating in (e.g. / or * for math).
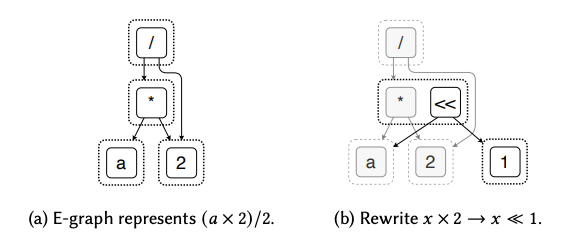
Instead of destructive rewrites over the tree of nodes, we can grow the e-graph by representing the transformed program as new equivalences. The following is an example of rewriting to be .
Originally, the e-class containing * just has one item which points to a and 2. We extend the e-class by adding << which points to a and 1, semantically saying that a * 2 is equivalent to a << 1. Note the Hash consing on the nodes to prevent duplication.
Finally, we can pick one ‘best’ e-node in each e-class. This is called ‘extracting’ the optimized term.