Convex

A set is convex if line between two points in the set stays in the set.

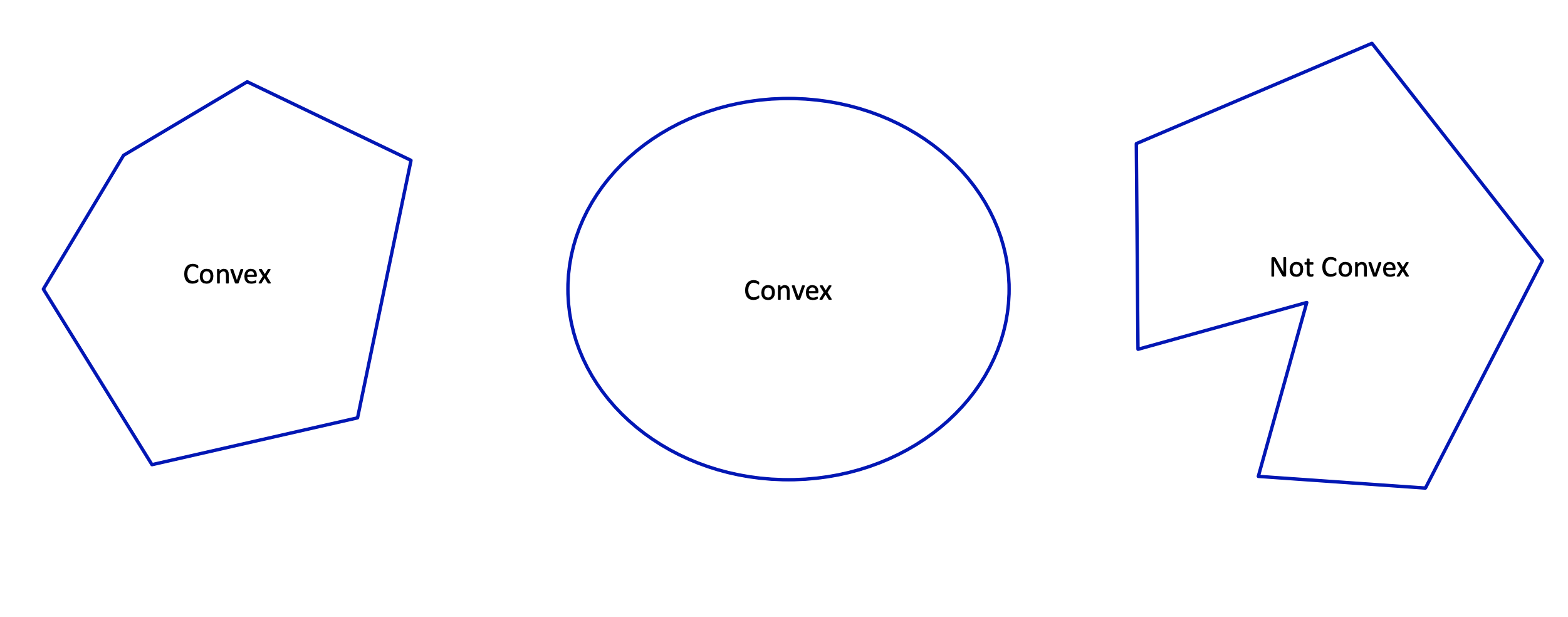
A function $f$ is convex if all the points above $f$ form a convex set. That is,

• If $f^{\prime \prime }(w)\ge 0,\forall w$
• A convex function multiplied by a non-negative constant is convex
• Norms and squared norms are always convex
• The sum of convex functions is convex
• The max of convex functions is a convex function
• The composition of a convex function $g$ and linear function $h$, $g\circ h$ is convex