Linear Algebra

A lot of content summarized from Mark Schmidt’s notes on Linear Algebra

Notation

Generally column major

• Scalar (1,1): $\alpha$
• Column Vector (m, 1): $\left[\begin{array}{c}{a}_1\\ a_2\end{array}\right]$
• Row Vector (1, n): $\left[\begin{array}{cc}{a}_1& a_2\end{array}\right]$
• Matrix (m, n): $\left[\begin{array}{cc}{a}_{1,1}& a_{2,1}\\ a_{1,2}& a_{2,2}\end{array}\right]$

Operations

Transpose

$(A^T{)}_{ij}=(A{)}_{ji}$

A matrix is symmetric if $A=A^T$

Vector Addition

Associative (brackets don’t matter) and commutative (order independent)

$a+b=\left[\begin{array}{c}{a}_1\\ a_2\end{array}\right]+\left[\begin{array}{c}{b}_1\\ b_2\end{array}\right]=\left[\begin{array}{c}{a}_1+b_1\\ a_2+b_2\end{array}\right]$

Scalar Multiplication

Associative (brackets don’t matter) and commutative (order independent)

$\alpha b=\alpha \left[\begin{array}{c}{b}_1\\ b_2\end{array}\right]=\left[\begin{array}{c}\alpha b_1\\ \alpha b_2\end{array}\right]$

Inner Product

Between two vectors of the same length, multiply each element together to get a scalar result

$a^{T}b={\sum }_{i=1}^n{a}_i{b}_i=\gamma$

A specific version of this is the dot product which can be expressed as the inner product between two vectors, $a\cdot b=a^{T}b$

• Commutative: $a^{T}b=b^{T}a$
• Distributive across addition: $a^T(b+c)=a^{T}b+a^{T}c$

Outer Product

Between two vectors of the same length, create a matrix multiplying each combination of elements in each vector.

Given two vectors $u=\left[\begin{array}{c}{u}_1\\ u_2\\ ⋮\\ u_m\end{array}\right]$ and $v=\left[\begin{array}{c}{v}_1\\ v_2\\ ⋮\\ v_n\end{array}\right]$,

$u\otimes v=A=\left[\begin{array}{cccc}{u}_1{v}_1& u_1{v}_2& \dots & u_1{v}_n\\ u_2{v}_1& u_2{v}_2& \dots & u_2{v}_n\\ ⋮& ⋮& \ddots & ⋮\\ u_m{v}_1& u_m{v}_2& \dots & u_m{v}_n\end{array}\right]$

The resulting matrix $A$ is always rank-1.

Multiplication

In general, we can multiply matrices A and B when the number of columns in A matches the number of rows in B

If A is (m, n) and B is (n, p), then AB is (m, p)

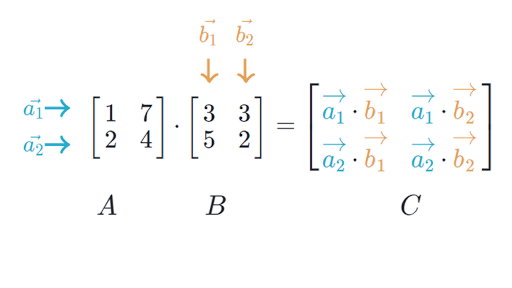
• Associative: $A(BC)=(AB)C$
• Distributive across addition: $A(B+C)=AB+AC$
• Generally not commutative: $AB\ne BA$
• Transposing reverses order: $(AB{)}^T=B^T{A}^T$
• Matrix powers don’t change order: $(AB{)}^2=ABAB$
• Matrix-vector multiplication always yields a vector: $x^{T}Ay=x^T(Ay)=(Ay{)}^{T}x=y^T{A}^{T}x$

Properties

Vector Norm

A scalar measure of a vector’s length

• $\Vert x\Vert \ge 0$

• $\Vert x{\Vert }_2^2=x^{T}x$

• Euclidean Norm (L2-Norm): $\Vert x{\Vert }_2=\sqrt{{\sum }_{i=1}^n{x}_i^2}$

  • Also note that $\Vert x{\Vert }^2=\Vert x{\Vert }_2^2=r^{T}r=⟨r,r⟩$

• Manhattan Distance (L1-Norm): $\Vert x{\Vert }_1=|r_1|+|r_2|$

  • How many ‘blocks’ you need to traverse

• L$\infty$-Norm: $\Vert x{\Vert }_{\infty }=\max (|r_1|,|r_2|)$

  • How many blocks you have to walk in any one dimensions

Rank

• The dimension of the vector space generated (or spanned) by its columns.
• This corresponds to the number of linearly independent columns of A.
  • This minimal set of vectors that span a space is called a basis

Orthogonal

If for some set of vectors $q$:

• $q_i^T{q}_j=0$, we call $q_i$ and $q_j$ orthogonal
• $q_i^T{q}_j=1$, we call $q_i$ and $q_j$ orthonormal

Inner product of square orthogonal matrices is the identity matrix: $Q^{T}Q=I=Q{Q}^T$

Linear Dependence

A vector is linearly dependent on a set of vectors if it can be written as a linear combination of them

$c={\alpha }_1{b}_1+{\alpha }_2{b}_2+\cdots +{\alpha }_n{b}_n$

A set of vectors is linearly dependent if and only if the zero vector can be written as a non-trivial combination of any of the vectors.

A matrix with fully independent columns has full column rank. If this is the case, $Ax=0$ implies that $x=0$

Special Matrices

Identity Matrix

1’s on the diagonal and 0’s otherwise. $I_n$ denotes an (n,n) identity matrix.

Multiplication by the identity matrix yields the original matrix. Columns of the identity matrix are called elementary vectors.

Diagonal Matrix

$D=\left[\begin{array}{ccc}{d}_1& 0& 0\\ 0& d_2& 0\\ 0& 0& d_3\end{array}\right]$

Spaces

Range (Column-space)

Subspace spanned by the columns of a matrix.

A system $Ax=b$ is solvable if and only if b is in $A$‘s column-space

Subspace

A non-empty subset of vector space that is closed under addition and scalar multiplication

Possible spaces of ${\mathbb{R}}^3$

• 0 Vector
• Any line or plane through the origin
• All of ${\mathbb{R}}^3$

We say that the vectors generate or span the subspace when you can reach any point in the subspace through a linear combination of the vectors.

Matrices as transformation

Viewing $Ax=T(x)$

A linear transformation can’t move the origin. But, if there are linearly dependent columns, there are non-zero vectors that can be transformed to zero. The set of vectors that can be transformed to 0 is called the null-space.

Null space: $\mathcal{N}(A)$ is all $x$ such that $Ax=0$

Fundamental Theorem of Linear Algebra

• $r$ is the dimension of the column-space which is the same as the dimension of the row-space
• The null-space is orthogonal to the row-space

Inverses

We can find the inverses if and only if A is square and doesn’t have null-space outside of the zero vector (otherwise we either lose information to the null-space or can’t get to all vectors)

If the inverse exists, it is a unique matrix such that $A^{-1}A=I=A{A}^{-1}$

Some identities

• $(A^{-1}{)}^T=(A^T{)}^{-1}$
• $(\gamma A{)}^{-1}={\gamma }^{-1}{A}^{-1}$
• Assuming both $A^{-1}$ and $B^{-1}$ exist, $(AB{)}^{-1}=B^{-1}{A}^{-1}$

Special inverses of diagonal matrices

$D=\left[\begin{array}{ccc}{d}_1& 0& 0\\ 0& d_2& 0\\ 0& 0& d_3\end{array}\right]$

$D^{{}^{-}1}=\left[\begin{array}{ccc}1/d_1& 0& 0\\ 0& 1/d_2& 0\\ 0& 0& 1/d_3\end{array}\right]$

Solving Linear Equations

Given A and b, we want to solve for x in $Ax=b$

Say, $\left[\begin{array}{cc}2& -1\\ 1& 1\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{c}1\\ 5\end{array}\right]$.

We can interpret this multiple ways:

1. By rows: $x$ is the intersection of the hyperplanes $2x-y=1$ and $x+y=5$
2. By columns: $x$ is the linear combination that yields the RHS in $x\left[\begin{array}{c}2\\ 5\end{array}\right]+y\left[\begin{array}{c}-1\\ 1\end{array}\right]=\left[\begin{array}{c}1\\ 5\end{array}\right]$
3. Transformation

$Ax=b$ generally has a solution when $b$ is in the column-space of A. It has a single unique solution if the columns of A are linearly independent.

If $Ax=b$ has as solution we say it is consistent.

Basically, $x=A^{-1}b$

We can solve using Gaussian Elimination