Functional Programming

Terminology

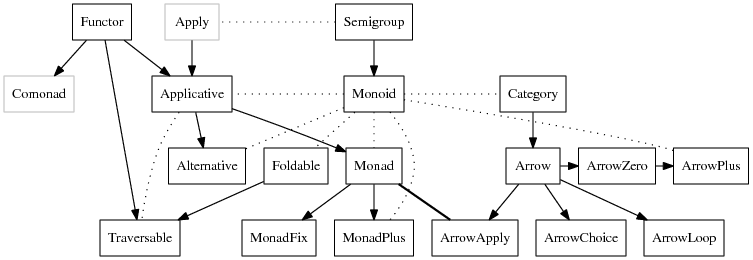
Category Theory

Category Theory to Haskell

• Objects are types
• Morphisms are functions
• Things that take a type and return another type are type constructors
• Things that take a function and return another function are higher-order functions
• Typeclasses capture the fact that things are often defined for a ‘set’ of objects at once

Functor

A ‘container’ of some sort, along with the ability to apply a function uniformly to every element in it

Essentially a transformation between categories. Given categories $C$ and $D$ and a functor $F:C\to D$

1. $F$ maps any object $A\in C$ to $F(A)\in D$ (the type constructor)
2. $F$ maps morphisms $f:A\to B\in C$ to $F(f):F(A)\to F(B)\in D$ (fmap). Importantly, this means that all functors must be generic over at least one parameter (e.g. Maybe and not Integer)
   • applying fmap is sometimes called ‘lifting’ as it lifts a function from the normal context into the ‘f’ world

class Functor f where
	-- fmap maps morphisms
	fmap :: (a -> b) -> f a -> f b
 
	-- applies a 'constant' function to replace the values in a container
	(<$) :: a -> f b -> f a
	-- default implementation
	(<$) = fmap . const

fmap takes a function which maps a value from a to b and applies it to a Functor f. Think of f as the container, (a -> b) as the function that operates on the ‘inner’ values.

Monad

Monads are functors from a category $A$ to that same category. A container for values that can be mapped over.

Think of it like a context-specific environment. You need a function to transform things outside of it to things in it. You also need a function to manipulate stuff inside of that environment.

A monad is a functor $M:C\to C$ along with two morphisms $\forall X\in C$

1. ${\text{unit}}_X:X\to M(X)$ (return)
2. ${\text{join}}_X:M(M(X))\to M(X)$ (can be recovered from bind)

class Monad m where
  -- join operation (optional, only one of bind or join need to be defined)
  join :: m (m a) -> m a
 
  -- bind operation
  -- takes an f :: (a -> m b) and applies it to
  -- the inner value a of m
  (>>=)  :: m a -> (a -> m b) -> m b
 
  -- replaces m a with m b
  (>>)   :: m a ->  m b       -> m b
 
  -- constructs the simplest monad m using a
  return ::   a               -> m a

Monad laws

return a >>= k                  =  k a
m        >>= return             =  m
m        >>= (\x -> k x >>= h)  =  (m >>= k) >>= h

Left and Right Associativity

Associativity of an operator determines how operators are grouped in the absence of parentheses.

For the following examples, we consider a fictional operator ~

1. Associative: operations can be grouped arbitrarily (e.g. addition, order doesn’t matter)
2. Left-associative: operations are grouped left to right
   1. a ~ b ~ c is interpreted as (a ~ b) ~ c
   2. Examples include
      1. Function application operator
3. Right-associative: operations are grouped right to left
   1. a ~ b ~ c is interpreted as a ~ (b ~ c)
   2. Examples include
      1. Variable assignment (=)
      2. Exponentiation (^)
4. Non-associative: operations cannot be chained

Parser Combinators

Parser combinators are a technique for implementing parsers by defining them in terms of other parsers

Notes on Chumsky

Where a and b are both parsers.

Parser Methods

1. just(a) accepts a single string a
2. a.or(b) parse a, if a fails, try parsing b
3. a.choice(b,c,d...) try parsing b, c, d, return first one that succeeds
4. a.or_not() optionally parse a
5. a.ignore_then(b) ignore pattern a then parse b
6. a.then_ignore(b) parse a then ignore b
7. a.then(b) parse both a and b and return a tuple of (a,b)
8. a.padded() ignore whitespace around a
9. a.repeated().at_least(n) parse a at least n times
10. a.filter(fn) only accept a if fn(a) evaluates to true

Result Methods

1. a.collect() turn results of a into an iterator
2. a.map(b) map results of a into type b
3. a.chain(b) concatenate results of parsers a and b into collection
4. a.copy(b) duplicate parser definition
5. a.flatten() flatten nested collection
6. a.to(b) marks result of a as type b
7. a.labelled(b) label result of a with b
8. a.end() indicate end of parser

Haskell Syntax Quirks

• $ :: (a -> b) -> a -> b is function application (adds implicit parentheses and makes it right associative instead of left associative)
  1. Normally, sort "abc" ++ "def" would be interpreted as (sort "abc") ++ "def"
  2. If we use the $ operator, we can do sort $ "abc" ++ "def" which is interpreted as sort ("abc" ++ "def") as intended.
• . is function composition. Read the dot as the little dot in $f\circ g$
• <> is a synonym for mappend :: Monoid m => m -> m -> m or the monoidal append
• <$> is a synonym for fmap :: (a -> b) -> f a -> f b
  • Intuitively like applying a function to a container
• <*> is like <$> but for wrapped functions (<*>) :: Applicative f => f (a -> b) -> f a -> f b
  • Intuitively like applying a function in a container to another container
• Remember that (<$) and ($>) point towards the value that will be kept
• void :: Functor f => f a -> f () is implemented as void x = () <$ x. Read as: whatever you give me, I will return the unit value