Regularization

A method for controlling complexity. Our main tools:

1. Model averaging (e.g. ensemble methods)
2. Regularization (this)

When we have multiple models with the same training models, we should pick models that are more conservative (e.g. in linear regression, pick smaller slope)

We should regularize $w_j$ so that they don’t explode.

Makes the tangent to the level curves of the gradient point towards the global minimum

L0-Regularization

• Adds penalty on number of non-zeros to select features

$f(w)=\mathcal{L}+\lambda \Vert w{\Vert }_0$

L2-Regularization (Ridge Regression)

• Generally decreases overfitting

$f(w)=\mathcal{L}+\frac{\lambda }{2}\Vert w{\Vert }^2$

This almost always decreases test error. Bigger $\lambda$ also means gradient descent converges faster.

To help with this, we can standardize continuous feature by replacing it with its z-score.

L1-Regularization (LASSO)

• Like L2-regularization, it’s convex and improves our test error
• Like L0-regularization, it encourages elements of $w$ to be exactly zero (though not as sparse)

$f(w)=\mathcal{L}+\lambda \Vert w{\Vert }_1$

We can actually combine this using an Ensemble method + bootstrapping (BoLASSO):

• Create bootstrap samples
• Run feature selection on each sample
• Take the intersection of selected features
• Reduces false positives

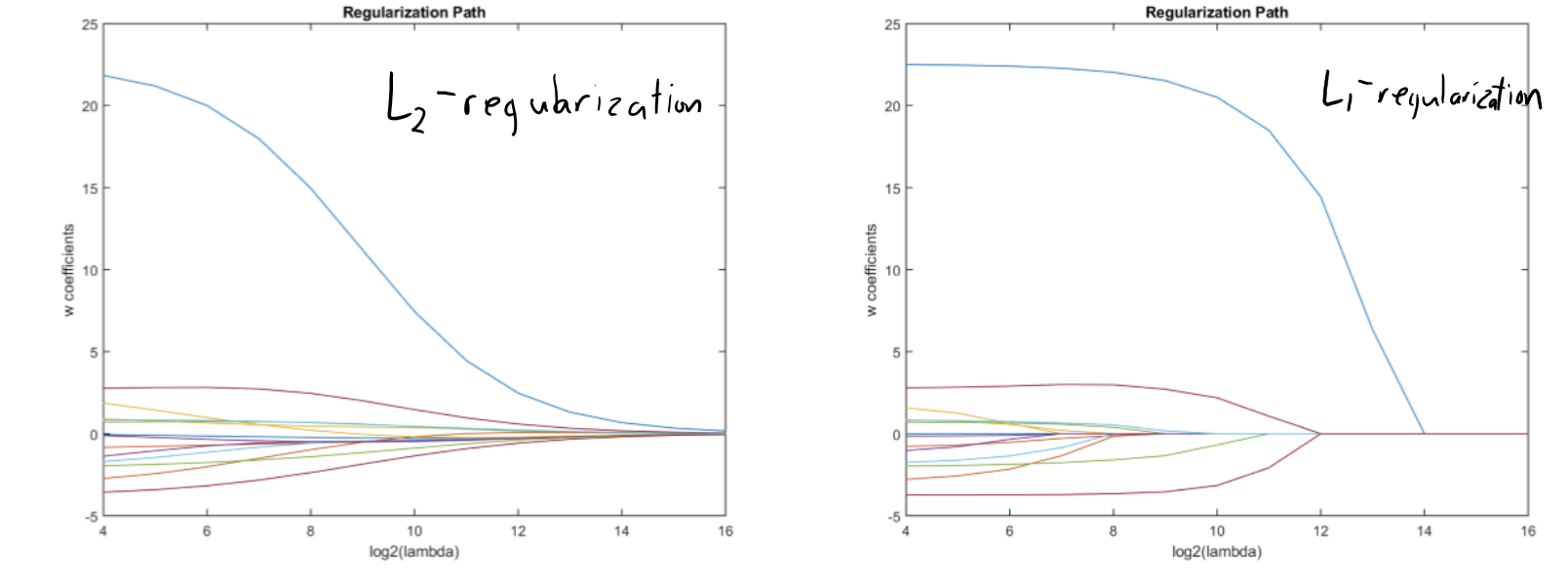
How is this different from L2?

The penalty stays is proportional to how far away $w_j$ is from zero. There is still something to be gained from making a tiny value exactly equal to 0.

With L2, the penalty gets smaller as you get closer to zero. The penalty asymptotically vanishes as $w_j$ approaches 0 (no incentive for “exact” zeroes).

L1-Regularization sets values to exactly 0, basically removing features from the model