Change of basis

Effectively by constructing new features that take the variable to certain powers. To get a y-intercept (bias), we just raise $x$ to the 0th power to get 1. We can fit polynomials of degree $p$ by raising other powers:

$$Z=\left[\begin{array}{ccccc}1& x_1& x_1^2& \dots & x_1^p\\ 1& x_2& x_2^2& \dots & x_2^p\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& x_n& x_n^2& \dots & x_n^p\end{array}\right]$$

As the polynomial degree increases, the training error goes down but the approximation error goes up.

Choosing a basis is hard! We can do something like Gaussian radial basis functions (RBFs) or polynomial basis as these are both universal approximators given enough data.

Kernel Trick

Let $Z$ be the basis. With multi-dimensional polynomial bases, actually forming $Z$ which is $k=O(d^p)$ is intractable.

Represent each column of $Z$ as a unique term. For example, with an $X$ of $d=2$, we can use $p=2$ to get

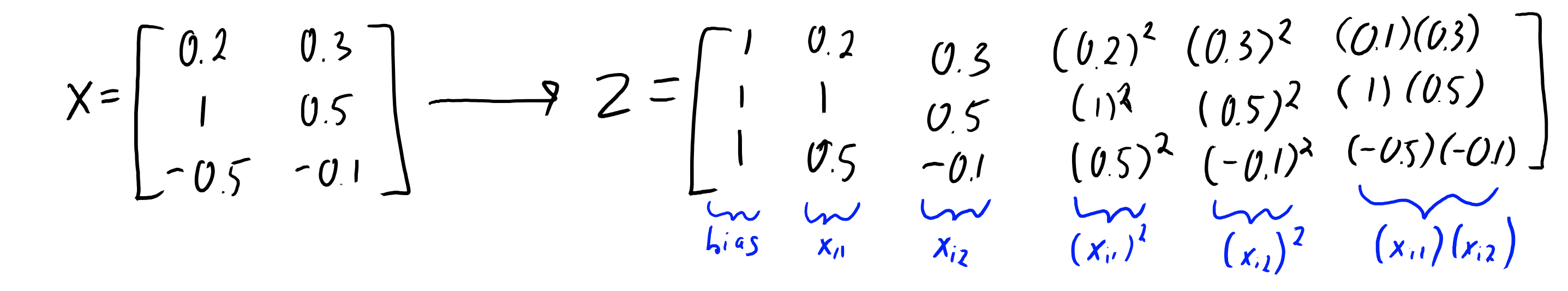
We compute $u=(K+\lambda I{)}^{-1}y$

and for testing:

$$\begin{array}{rlr}\hat{y}& =\tilde{Z}v& \\ & =\tilde{Z}{Z}^T(Z{Z}^T+\lambda I{)}^{-1}y& \text{minimum of L2-regularized least squares: }v=Z^T(Z{Z}^T+\lambda I{)}^{-1}y\\ & =\tilde{K}(K+\lambda I{)}^{-1}y& \\ & =\tilde{K}u& u\text{ is a (n,1) of kernel weights we learn}\end{array}$$

The key idea behind “kernel trick” for certain bases (like polynomials) is that we can efficiently compute $K$ and $\tilde{K}$ even though forming $Z$ and $\tilde{Z}$ is intractable.

We call $K=Z{Z}^T$ the Gram Matrix.

Finally, we call the general degree-p polynomial kernel function $K_{ij}=k(x_i,x_j)=(1+x_i^T{x}_j{)}^p$. Computing $k$ is only $O(d)$ time instead of $O(d^p)$.

Thus, computing $K$ is $O(n^{2}d+n^3)$:

1. Forming $K$ takes $O(n^{2}d)$ time
2. Inverting $K+\lambda I$ which is a $(n,n)$ takes $O(n^3)$

All of our distance-based methods have kernel versions

Learned Basis

We can also learn basis from data as well. See latent-factor model