Latent-Factor Models

Like change of basis but instead of hand-picking the features, we learn them from data.

Part weights are a change of basis from $x_i$ to some $z_i$. The canonical example is Principal Component Analysis (PCA)

PCA

PCA is parametric and does not provide unique global optimum.

Takes in a matrix $X$ and an input $k$ and outputs two matrices such that $X\approx ZW$:

• $Z$ is a (n,k) matrix. Each row $z_i$ is a set of features/part weights
• W is a (k,d) matrix. Each row $w_c$ is a part/factor/principle component
  • We can think of $W$ as rotating data so that the slope is zero
• Approximation of one ${\hat{x}}_{ij}$ is $(w^{j^T}{z}_i)=⟨w^j,z_i⟩$
  • Each $x_i$ can be thought of as a linear combination of all the factors

Assumptions:

• Assumes $X$ is centered (each column of $X$ has a mean of zero)

Use cases:

• Dimension reductionality: Effectively allows us to reduce the dimensionality of X if $k<d$
  • Actually, it only ever makes sense if $k\le d$
• Outlier detection: if PCA gives a poor approximation, $x_i$ could be an outlier
• Data visualization: $k=2$ to visualize high-dimensional objects

We minimize

$$\begin{array}{rlr}f(W,Z)& =\sum _{i=1}^n\sum _{j=1}^d(⟨w^j,z_i⟩-x_{ij}{)}^2& \text{Approximating }{x}_{ij}\text{ by }⟨w^j,z_i⟩\\ & =\sum _{i=1}^n\Vert W^T{z}_i-x_i{\Vert }^2& \text{Approximating }{x}_i\text{ by }{W}^T{z}_i\\ & =\Vert ZW-X{\Vert }_F^2& \text{Approximating }X\text{ by }ZW\end{array}$$

If we do alternating minimization,

1. Fix Z and optimize W: ${\nabla }_{w}f(W,Z)=Z^{T}ZW-Z^{T}X$
2. Fix W and optimize Z: ${\nabla }_{w}f(W,Z)=ZW{W}^T-X{W}^T$

We converge to a local optimum which will be a global optimum if W and Z are randomly initialized (if you don’t pick a saddle point)

For large X, we can also just use SGD and cost per iteration is only $O(k)$

Choose $k$ by variance explained

How much of the variance can be explained by the choice of factors?

For a given $k$, we compute the variance of the errors over the variable of each given $x_{ij}$

$\frac{\Vert ZW-X{\Vert }_F^2}{\Vert X{\Vert }_F^2}$

Uniqueness

Optimal $W$ is non-unique:

1. Scaling problem: Can multiply any $w_c$ by any non-zero $\alpha$
2. Rotation problem: Can rotate any $w_c$ within the span
3. Label switching problem: Can switch any $w_c$ with any other $w_c$

To help with uniqueness,

1. Normalization: We ensure $\Vert w_c\Vert =1$
2. Orthogonality: We enforce $w_c^T{w}_{c^{\prime }}=0$ for all $c\ne c^{\prime }$
3. Sequential fitting, we fit each $w_i$ in sequence

Multi-Dimensional Scaling

Gradient descent on points on a scatter point; try to make scatterplot distances match high-dimensional distances

$f(Z)={\sum }_{i=1}^n{\sum }_{j=i+1}^n(\Vert z_i-z_j\Vert -\Vert x_i-x_j\Vert {)}^2$

No $W$ matrix needed! However, cannot be done using singular value decomposition (a matrix factoring technique). We need gradient descent.

• Non convex
• Sensitive to initialization
• Unfortunately, MDS often does not work well in practice; MDS tends to “crowd/squash” all the data points together like PCA.

t-SNE

t-Distributed Stochastic Neighbour Embedding

However, using Euclidean (L2-norm) may not be a great representation of data that lives on low-dimensional manifolds. In these cases, Euclidean distances make sense “locally” but Euclidean distances may not make sense “globally”.

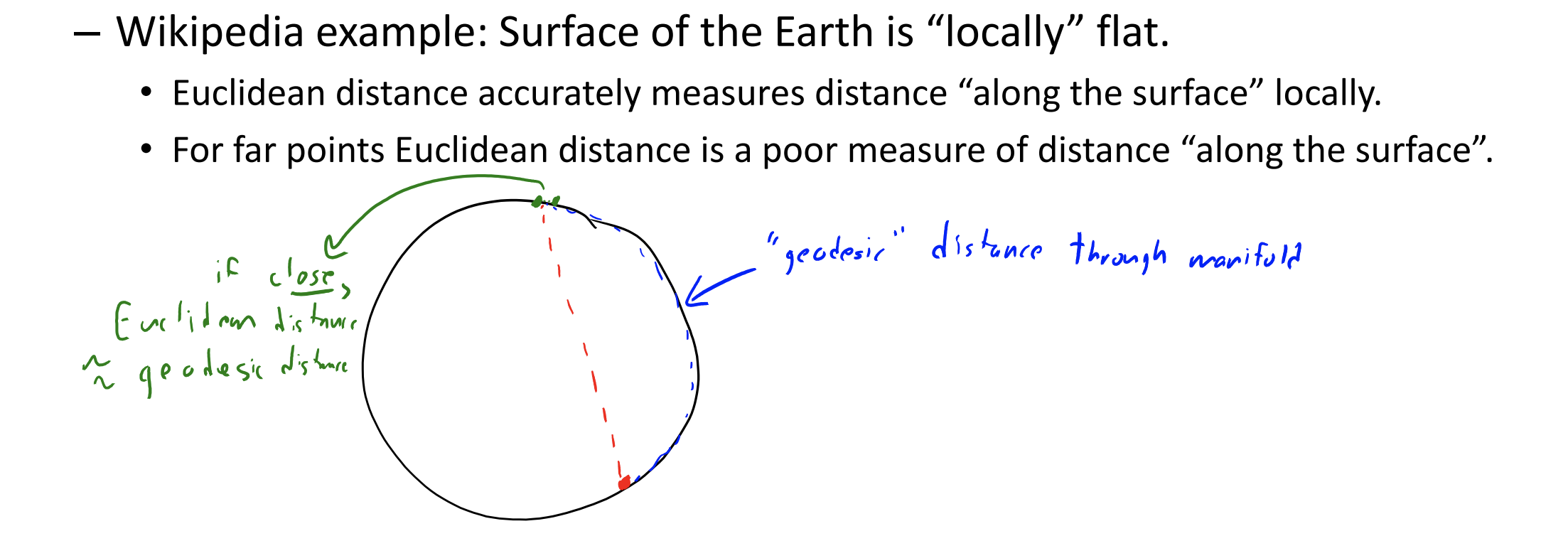
t-SNE is actually a special case of Multi-Dimensional Scaling. The key idea is to focus on distance to “neighbours”, allowing gaps between distances to grow

Word2Vec

Each word $i$ is represented by a vector of real numbers $z_i$

Trained using a masking technique.

• Takes sentence fragments and hides/masks a middle word
• Train so that $z_i$ of hidden word is similar to $z_i$ of surrounding words

$$p(z_i)=\prod _{j\in \text{surrounding}}\frac{\exp (z_i^T{z}_j)}{{\sum }_{c=1}^{\text{\# words}}\exp (z_c^T{z}_j)}$$

Gradient descent on for $-\log (p(z_i))$