Clocks

Measuring time in the context of computer systems

Physical Time

Two types of clock

1. Physical clock: number of seconds elapsed
2. Logical clock: count events, e.g. messages sent

Time is hard! So many different ways of measuring time

• Greenwich Mean Time (GMT): the normal human time format, based on Earth rotation
• International Atomic Time (TAI): some multiple of Caesium-133 resonant frequency
• Compromise, UTC is TAI with corrections to account for Earth rotation
• Unix Time: number of seconds since the epoch (Jan 1, 1970) not counting leap seconds
• ISO8601: year, month, day, hour, minute, second, and timezone offset relative to UTC

We periodically adjust our local clocks with a server that has a more accurate time source using Network Time Protocol (NTP) or Precision Time Protocol (PTP)

Logical Time

Computers typically have a service like NTP which synchronizes computer clocks with well known time sources on the internet. Because of this, two consecutive readings of the system time on a given server can have time going backwards. As there is no upper bound on clock drift across servers, it is impossible to trust timestamps on two different servers as a way to infer causality!

We use logical clocks to work based off of the number of events that have occurred rather than actual time passed.

Lamport Clocks

Provides a partial order on events

Logic

• On initialization, set t := 0 for each node
• On any event on local node, fn tick() -> t += 1
• On sending message $m$, fn send(m) -> tick(); actually_send(t, m)
• On receiving fn receive(t', m) -> t = max(t, t') + 1; do_something(m)

Properties

• If $a\to b$ then $L(a)<L(b)$
• However, $L(a)<L(b)$ does not imply $a\to b$
• Possible that $L(a)=L(b)$ for $a\ne b$

This means that two identical Lamport timestamps might not correspond to the same unique event. However if we include the node $N(e)$ for the node where event $e$ occurred, then $(L(e),N(e))$ uniquely identifies event $e$.

We attempt to define a total causal order

$(a\prec b)⟺(L(a)<L(b))\vee (L(a)=L(b)\wedge N(a)<N(b))$

However even now, given timestamps $L(a)<L(b)$, we can’t tell whether $a\to b$ or $a\parallel b$

To separate causality from concurrent events, we need vector clocks!

Vector Clocks

Provides a causal order on events

Instead of having a single counter t for all nodes, we keep a vector timestamp $a$ of an event for each node so we have $V(a)=⟨t_1,t_2,\dots ,t_n⟩$ where $t_i$ is the number of events observed by node $N_i$

Each node has a current vector timestamp $T$, on an event on node $N_i$, increment vector element $T[i]$

Logic

• On initialization , set t := [0] * n
• On any event on node $N_i$, fn tick() -> t[i] += 1
  • Each time a process experiences an internal event, it increments its own clock in the vector by one
• On sending message $m$ from node $N_i$, fn send(m) -> tick(); actually_send(t, m)
• On receiving fn receive(t', m) -> t = tick(); zip(t, t').map(max); do_something(m)

Thus, a vector timestamp of an event $e$ actually represents all of its causal dependencies: $\{e\}\cup \{a|a\to e\}$

E.g. $⟨2,2,0⟩$ represents first two events from $N_1$, first two events from $N_2$, and no events from $N_3$

Ordering

• $T=T^{\prime }⟺T[i]=T^{\prime }[i]\forall i\in \{1,\dots ,n\}$ (T and T’ are same if each element has the same value)
• $T\le T^{\prime }⟺T[i]\le T^{\prime }[i]\forall i\in \{1,\cdots ,n\}$ (T happened at the same time or earlier than T’ if each element in T is less than or equal to its value in T’)
• $T<T^{\prime }⟺T\le T^{\prime }\wedge T\ne T^{\prime }$ (T happened earlier than T’ if each element in T is less than its value in T’, at least one element in T differs from T’)
  • $T\parallel T^{\prime }⟺T\nleqq T^{\prime }\wedge T^{\prime }\nleqq T$ (T is incomparable to T’)

Properties (based on Order theory)

• $V(a)\le V(b)⟺(\{a\}\cup \{e|e\to a\})\subseteq (\{b\}\cup \{e|e\to b\})$
• $V(a)<V(b)⟺(a\to b)$
• $V(a)=V(b)⟺(a=b)$
• $V(a)\parallel V(b)⟺a\parallel b$

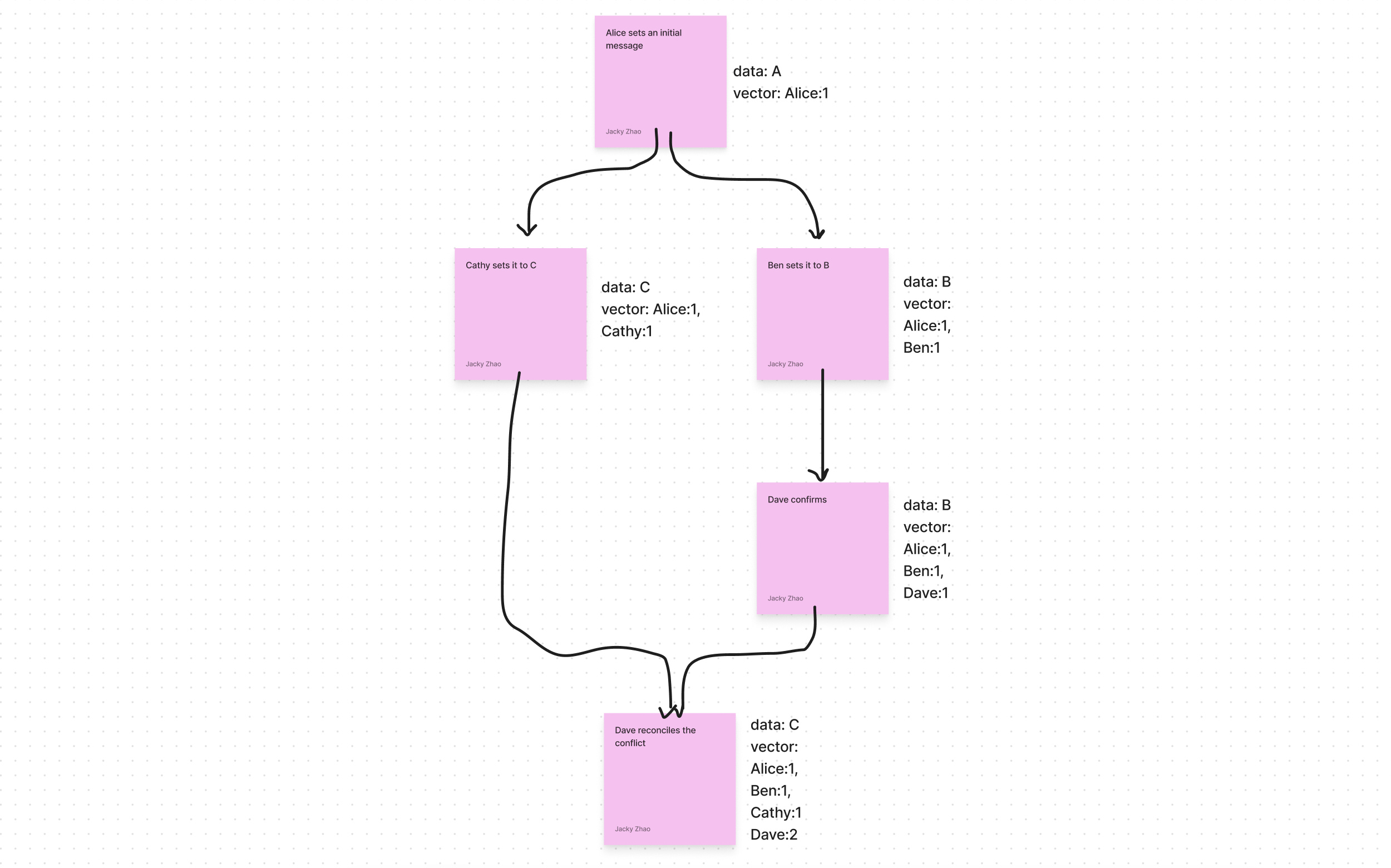
You can tell that versions are in conflict when neither vector clock “descends” from the other. In order for vector clock B to be considered a descendant of vector clock A, each marker in vector clock A must have a corresponding marker in B that has a revision number greater than or equal to the marker in vector clock A. Markers not contained in a vector clock can be considered to have revision number zero.

Vector Clock Example

Hybrid Logical Clocks

Physical and logical clocks both have non-ideal properties.

• Logical clocks don’t actually store any sort of date-time when events happen. Clients usually have a notion of time through actual wall time
• BUT wall time isn’t perfect either as clock drift is non-trivial and users can manually turn time backwards on their local machines

Note that this is not a substitute for Vector Clocks as they only provide partial order instead of causal order

Can we combine them to achieve better properties?

Hybrid Logical Clocks (HLCs) achieve

• partial ordering
• constant space
• bounded different from physical time

We can store a tuple containing:

• pt: physical time (wall time)
• l: logical time (holds maximum pt so far)
• c: capturing causality when l is equal

This tuple can be used directly as a replacement for a physical clock timestamp (and in fact works as a superposition on top of the NTP protocol without any interference)

Pseudocode

• Initial state
  • l := 0
  • c := 0
• Send / local event
  • l' := l
  • l := max(l', pt) update l to pt if applicable
  • if pt is the same (l == l'):
    • c += 1 increment causality as logical time is the same
  • if pt is updated:
    • c := 0 reset c
  • timestamp message with (l, c)
• Receive of message m
  • l' := l
  • l := max(l', m.l, pt)
  • if all logical clocks are the same l == l' == m.l:
    • c := max(c, m.c) + 1 set to max causality known
  • if our logic clocks are the same but message logical clock is behind l == l':
    • c += 1 (ignore as message clock is behind)
  • if our logic clock was behind the message logical clock and just got updated l == m.l
    • c := m.c + 1
  • otherwise pt was just updated
    • c := 0 reset c
  • timestamp message with (l, c)